Xinwei (David) Yao

Mathematics  •  Computer Science  •  Film

AI Video Generation at YouTube & DeepMind

About Me

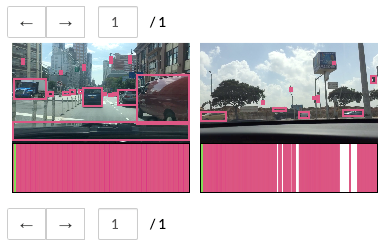
Hi! My name is Xinwei (David) Yao. I am currently a researcher at DeepMind where I work on bringing state-of-the-art generative AI to content creators. Most recently I have been working on Veo for text-to-video, image-to-video and various control capabilities such as camera, reference, speech. We have launched some of these features to YouTube, Flow, Gemini and Google Cloud, empowering a wide range of use cases from casual creators to professional filmmakers to media enterprises.


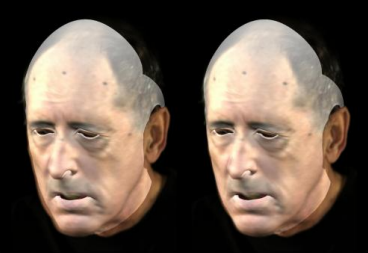
I am interested in applied research and building products in the space of generative AI for visual media, and specifically in video effects and visual storytelling. Previously I was a Computer Science PhD candidate at Stanford University advised by Kayvon Fatahalian, researching Computer Vision and Graphics applications to video and film, and in particular video analysis and synthesis (Deepfake generation). I received my B.S. degree in both Intensive Mathematics and Computer Science from Yale University in 2016.


I am an experienced Software Engineer on both consumer and enterprise AI products and large-scale distributed infrastructure systems. Before my current work with Google Deepmind on foundational video generation models, I led the Computer Vision infrastructure team for Document AI and Vision API for enterprise customers from 2021 to 2023 at Google Cloud AI. From 2016 to 2018 at Google in New York City I worked on a planet-scale Search Engine platform powering hundreds of Google products including WebSearch and YouTube, the two largest search engines on the Internet, serving 107s of search queries every second.


I enjoy teaching and giving talks. I gave a SIGGRAPH 2021 talk on my deepfake paper and was the head TA for CS248: Interactive Computer Graphics at Stanford in Winter 2020. At Google, I have lectured on topics ranging from AI Hardware, Vision Transformers for Generative AI and have taught internal Machine Learning Engineering courses, and the anatomy of the Web Search Engine to new hires with great success. At Yale Math Department, I have written expositions and given seminar lectures on topics including Network Algorithms, Graph Theory and Galois Theory. The lecture notes and essays can be found here.


Born and raised in Nanjing, China, I can speak Mandarin, English and Spanish and I love travelling to different places. In my free time, I am a cinephile and I watch movies from all over the world but mostly from US, Europe and East Asia. I especially enjoy horror films and coming-of-age comedies. I write about them too, usually short comments but sometimes longer reviews.

Research and Software Projects

Text2Vid

Text-based Editing of Talking-heads

Research on a tool for fast generation of talking-heads from text inputs using only 2-3 minutes of reference video data.

Esper

Esper

Research on large-scale video analysis and synthesis with compositions of spatiotemporal labels

Deep Energies

Deep Energies for Estimating 3D Facial Pose and Expression

Research on face tracking for film special effects

Shadow-Play

Shadow-Play

A Qt program to view shadows of rotated 3D models

Envy-My-Simplex

Envy My Simplex

A WebGL First-person shooter game

Midi-Visualizer

MIDI Visualizer

A Haskell program for visualizing midi files

Shifts

Shifts

A Ruby on Rails application that allows easy tracking of employees who work scheduled and even unscheduled hours in various locations and times.

GenoWAP

GenoWAP

A Rails back-end and a Python front-end that implements an empirical Bayesian approach for prioritizing SNPs in GWAS.

Bookmark+

Bookmark+

A chrome extension that saves webpages, quotes, images and videos.

Teaching

C++ Mentorship Program 2021.7-Present

C++ Mentor and Readability Approver at Google

CS 248: Interative Computer Graphics Winter 2020

Teaching Assistant for Kayvon Fatahalian's course at Stanford University

New Googler Orientation: Life of a Query (How Search Works) 2018.5-2018.6

Instructor at Google New York

MATH 370: Galois Theory Spring 2016

Grader for Miki Havlickova's course at Yale University

CPSC 365: Design and Analysis of Algorithms Spring 2016, Spring 2015

Peer Tutor for Daniel Spielman's course at Yale University

CPSC 202: Mathematical Tools for Computer Science Fall 2015

Peer Tutor for Dana Angluin's course at Yale University

Talks

TPUs, How do They Work? 2024.4

Three-Part Lecture in YouTube Advanced Capabilities and Effects Group on Google's TPU hardware for AI.

Applying Transformers to Computer Vision 2024.3

Invited Lecture in YouTube Advanced Capabilities and Effects Group for Part II of its Generative Vision Fundamental Series.

Iterative Text-based Editing of Talking-heads using Neural Retargeting 2021.8

Invited Talk in Chris Bregler's team at Google Research on my TOG 2021 paper.

Iterative Text-based Editing of Talking-heads using Neural Retargeting 2021.8

Invited Speaker at SIGGRAPH 2021 Video Editing Panel on my TOG 2021 paper.

Iterative Text-based Editing of Talking-heads using Neural Retargeting 2021.7

Invited Talk at Google Cloud AI Vision/Video Team on my TOG 2021 paper.

Iterative Text-based Editing of Talking-heads using Neural Retargeting 2021.7

Invited Talk at RunwayML on my TOG 2021 paper.

Interactive Tool for Talking Head Video Synthesis from Text 2019.12

GCafe Talk at Stanford Graphics Lab on a paper in preparation that extends Fried et al. (2019)

Design Considerations for kNN in a Search Engine 2019.10

Talk in Kayvon Fatahalian's research group at Stanford University.

Easier and Faster Text-based Editing of Talking Head Video 2019.6

Talk in Maneesh Agrawala's research group at Stanford University on preliminary results of improvements to Fried et al. (2019)

p-adic Numbers and Bruhat-Tits Tree 2016.2

Lectures in Igor Frenkel's course MATH 480: Senior Seminar: Mathematical Topics at Yale University.

Back-Pressure in Traffic Signal Control 2015.5

Talk in Leandros Tassiulas' course ENAS963: Network Algorithms and Stochastic Optimization at Yale University.

Math Notes

Casus irreducibilis, Latin for "irreducible case", states that an irreducible cubic polynomial with three real roots cannot have any of its roots expressible by only taking real radicals. Although all roots are real, one must introduce complex valued expressions to write them down using rational numbers and radicals.

I first came across this theorem when I was doing homework for Galois Theory. I was curious to see the proof but I could find no complete and correct proof of this result online. Luckily I found the proof explained in the Abstract Algebra textbook by Dummit and Foote.

Here is a complete proof.

In February 2016, I gave a series of 3 lectures for the class MATH480 (Senior Seminar: Mathematical Topics) on the topic of p-adic numbers, their construction by completing the field of rational numbers, and the Bruhat-Tits tree associated with the 2-dimensional p-adic integer lattices.

Here are the lecture notes.

In the fall of 2015, I did a senior thesis research project with advisor Daniel A. Spielman on the hardness of the l0-regularization problem of finding smooth extensions of functions on graphs, where one is given the function value at some initial vertices and an integer k and needs to compute the function that minimizes the Laplacian quadratic form while coinciding with all but k of the initial values. Kyng et al. (2015) proved that the problem is NP-hard by reducing from the problem of finding the minimum bisection of a graph. The thesis gives a new reduction from min-bisection that yields further result on the relation between hardness of approximating the regularization problem and hardness of solving or approximating min-bisection for special graphs.

Here is my thesis.

In May 2015, I gave a talk for the class ENAS963 (Network Algorithms and Stochastic Optimization) on the topic of traffic signal control methods based on the Back-Pressure algorithm proposed by Tassiulas et al. in 1992.

Here are the notes for the talk.